02. 알고리즘 시간 복잡도 함수(2)

(해당 내용은 "C++로 쉽게 플어쓴 자료구조(천인국, 최영규 저, 2016)"을 기반으로 작성되었습니다.)

(해당 내용은 자료구조/알고리즘을 공부하기 위해 작성된 것이므로, 내용에 오류가 있을 수 있습니다.)

 

이전 포스팅에서 시간 복잡도 함수를 구해 보았습니다.

2022.11.16 - [자료구조, 알고리즘] - 02. 알고리즘 시간 복잡도 함수(1)

02. 알고리즘 시간 복잡도 함수(1)

시간 복잡도 표현 방법

이 시간 복잡도 함수 T(n)은 입력 방식에 따라 복잡한 수식이 될 수 있습니다만

자료의 개수가 점점 늘어나고, 입력값 n의 값이 점차 커지면 최고차항의 영향이 다른 항에 비해 커지게 됩니다.

 

예를 들어 T(n) = n² + n + 1이란 함수가 있다고 가정해 봅시다.

n = 1이면, T(n)은 1 + 1 + 1 = 3이 됩니다.

n = 10이면, T(n)은 100 + 10 + 1 = 111이 됩니다.

n = 100이면, T(n)은 10000 + 100 + 1 = 10101이 됩니다.

이처럼 n의 값이 커질수록 T(n)은 점점 커지게 되며, 최고차항과 유사한 값을 얻게 되므로,

결국 최고차항만으로도 시간 복잡도 분석에 충분하다는 결론을 얻게 됩니다.

 

이와 같이 불필요한 항과 계수를 제거하여 최고차항만으로 시간 복잡도를 평가합니다.

 

1) 빅오 표기법(Big O Notation) : 최악의 경우, 가장 널리 사용

알고리즘이 계산되는 경우 중 가장 오랜 시간이 걸리는 경우(최악의 경우)를 가정한 것입니다.

대부분의 경우 서비스를 준비할 때 가장 최악의 상황까지 고려하면서 준비하는 것이 가장 좋으므로,

알고리즘에서도 빅오 표기법을 알고리즘의 시간 복잡도를 평가하는 가장 중요한 척도로 사용됩니다.

 

2) 빅세타 표기법(Big Θ Notation) : 평균적인 경우

알고리즘이 계산되는 모든 경우에 대한 평균을 나타낸 것입니다.

그러나 최악의 경우를 반영하지 못하는 점에서 많이 고려되는 부분은 아닙니다.

 

3) 빅오메가 표기법(Big Ω Notation) : 최선의 경우

알고리즘이 가장 빨리 계산되는 경우를 나타낸 것입니다만,

알고리즘은 최선보다는 최악을 더 중요시하기 때문에 의미는 거의 없습니다.

빅오 표기법의 수학적 정의

빅 오 표기법의 수학적 정의는 아래와 같습니다.

두 개의 함수 f(n)과 g(n)이 주어졌을 때 모든 n>n₀에 대해 |f(n)| ≤ |cg(n)|을 만족하는 상수 c와 n₀가 존재하면 f(n) = O(g(n))이다.

예를 들어, f(n)=n²+2n+20과 g(n)=n²가 있다고 가정합시다.

만약 c가 3이라면, n이 n₀ 이상이 되는 지점부터 f(n)보다 cg(n)이 무조건 커지게 됩니다.

즉, 시간복잡도 f(n)이 최악의 상황이 되더라도 n₀보다 큰 n값을 입력하였다면 cg(n)을 넘을 수 없다는 뜻이 됩니다.

이런 경우, 빅오 표기법을 사용하여 O(g(n)), 즉 O(n²)라고 표기할 수 있는 것입니다.

빅오 표기법의 표기

빅오 표기법은 불필요한 부분을 제거하고, 시간 복잡도를 간편하게 비교하는 데에 목적이 있습니다.

1. 최고차항을 제외한 모든 항 제외

최고차항을 제외한 항들은 n의 크기가 커질수록 그 영향이 점점 줄어들기 때문에,

빅오 표기법에서는 최고차항을 제외한 모든 항은 제외합니다.

ex) f(n) = n⁵+4n⁴+10n³+20n²+50n+100 → O(n⁵)

2. 항의 계수 제외

시간 복잡도는 데이터 값(n)의 크기에 영향을 받으며, n이 커질수록 항의 계수는 영향이 점점 줄어든다고 가정하므로,

빅오 표기법에서는 항의 계수를 제외합니다.

ex) = 255n⁴ → O(n⁴)

시간 복잡도 함수 그래프

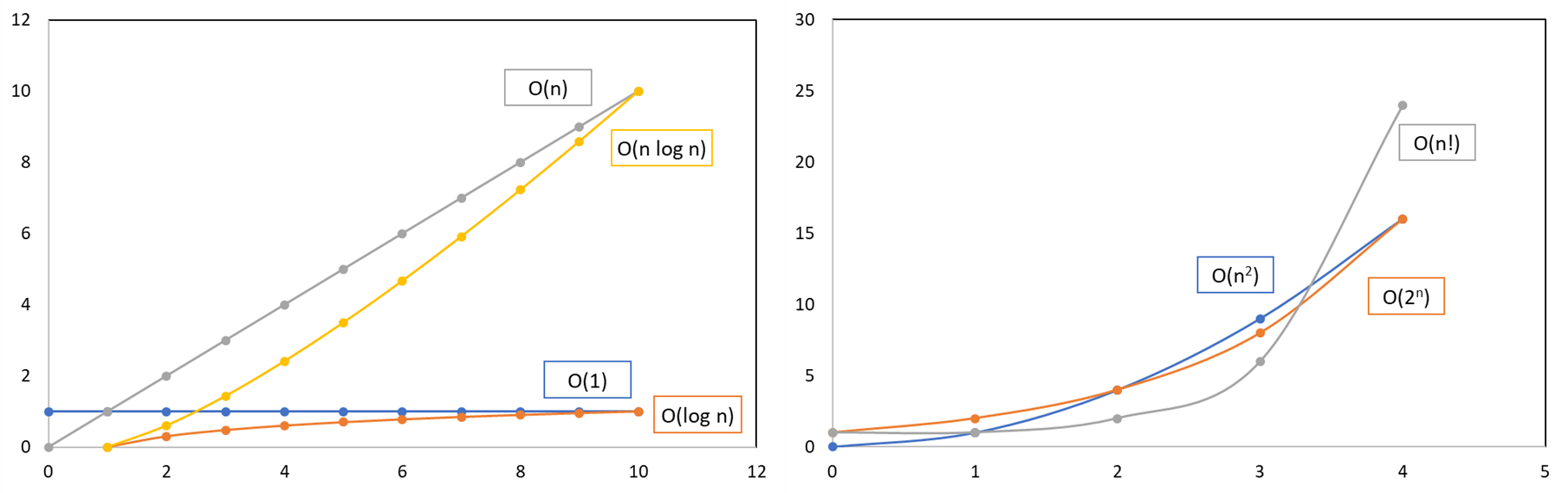
시간 복잡도를 나타낼 때 가장 많이 사용되는 빅오 표기법은 아래와 같으며, 아래로 갈수록 시간 복잡도가 높습니다.

• O(1) :  상수항이며, 스택이나 큐 등을 표현
• O(log n) : 로그함수이며, 이진 트리를 표현
• O(n) : 선형함수이며, for문을 표현
• O(n log n) : 선형 로그함수이며, 퀵 정렬, 힙 정렬, 합병 정렬을 표현
• O(n²) : 이차함수이며, 이중 for문이나 삽입 정렬, 버블 정렬을 표현
• O(2ⁿ) : 지수형이며, 피보나치 수열을 표현
• O(n!) : 팩토리얼

 

참고하면 좋은 글들

1. https://medium.com/humanscape-tech/%EC%BD%94%EB%93%9C%EC%9D%98-%EC%8B%9C%EA%B0%84-%EB%B3%B5%EC%9E%A1%EB%8F%84-%EA%B3%84%EC%82%B0%ED%95%98%EA%B8%B0-b67dd8625966

코드의 시간 복잡도 계산하기

2. https://velog.io/@dvot007/%EC%8B%9C%EA%B0%84-%EB%B3%B5%EC%9E%A1%EB%8F%84Big-O-%ED%91%9C%EA%B8%B0%EB%B2%95-%EA%B3%84%EC%82%B0

시간 복잡도 정리